SLWS207B May   2008  – January 2016 ADS5560 , ADS5562

PRODUCTION DATA.  

  1. 1 Features
  2. 2 Applications
  3. 3 Description
  4. 4 Revision History
  5. 5 Pin Configuration and Functions
  6. 6 Specifications
    1. 6.1  Absolute Maximum Ratings
    2. 6.2  ESD Ratings
    3. 6.3  Recommended Operating Conditions
    4. 6.4  Thermal Information
    5. 6.5  Electrical Characteristics
    6. 6.6  AC Electrical Characteristics for ADS5560 Fs = 40 MSPS
    7. 6.7  AC Electrical Characteristics for ADS5562, Fs = 80 MSPS
    8. 6.8  Electrical Characteristics for ADS5562
    9. 6.9  Electrical Characteristics for ADS5560
    10. 6.10 Digital Characteristics
    11. 6.11 Timing Characteristics for LVDS and CMOS Modes
    12. 6.12 Serial Interface Timing Characteristics
    13. 6.13 Reset Timing
    14. 6.14 Timing Characteristics at Lower Sampling Frequencies
    15. 6.15 Typical Characteristics
      1. 6.15.1 ADS5562 - 80 MSPS
      2. 6.15.2 ADS5560 - 40 MSPS
      3. 6.15.3 Valid Up to Max Clock Rate (ADS5562 or ADS5560)
  7. 7 Detailed Description
    1. 7.1 Overview
    2. 7.2 Functional Block Diagram
    3. 7.3 Feature Description
      1. 7.3.1 Low-Frequency Noise Suppression
      2. 7.3.2 Analog Input Circuit
        1. 7.3.2.1 Drive Circuit Recommendations
        2. 7.3.2.2 Example Driving Circuit
        3. 7.3.2.3 Input Common-Mode
        4. 7.3.2.4 Programmable Fine Gain
    4. 7.4 Device Functional Modes
      1. 7.4.1 Low Sampling Frequency Operation
      2. 7.4.2 Clock Input
        1. 7.4.2.1 Power-Down
          1. 7.4.2.1.1 Global STANDBY
          2. 7.4.2.1.2 Output Buffer Disable
          3. 7.4.2.1.3 Input Clock Stop
        2. 7.4.2.2 Power Supply Sequence
      3. 7.4.3 Output Interface
        1. 7.4.3.1 DDR LVDS Outputs
        2. 7.4.3.2 LVDS Buffer Current Programmability
        3. 7.4.3.3 LVDS Buffer Internal Termination
        4. 7.4.3.4 Parallel CMOS
        5. 7.4.3.5 Output Clock Position Programmability
      4. 7.4.4 Output Data Format
      5. 7.4.5 Reference
        1. 7.4.5.1 Internal Reference
        2. 7.4.5.2 External Reference
    5. 7.5 Programming
      1. 7.5.1 Device Programming Modes
      2. 7.5.2 Using Parallel Interface Control Only
        1. 7.5.2.1 Using Serial Interface Programming Only
        2. 7.5.2.2 Using Both Serial Interface And Parallel Controls
        3. 7.5.2.3 Description of Parallel Pins
      3. 7.5.3 Serial Interface
      4. 7.5.4 Register Initialization
    6. 7.6 Register Maps
      1. 7.6.1 Register Description
  8. 8 Application and Implementation
    1. 8.1 Application Information
    2. 8.2 Typical Application
      1. 8.2.1 Design Requirements
      2. 8.2.2 Detailed Design Procedure
        1. 8.2.2.1 Clocking Source for ADC5562
        2. 8.2.2.2 Amplifier Selection
      3. 8.2.3 Application Curve
  9. 9 Power Supply Recommendations
  10. 10Layout
    1. 10.1 Layout Guidelines
      1. 10.1.1 Supply Decoupling
      2. 10.1.2 Exposed Thermal Pad
    2. 10.2 Layout Example
  11. 11Device and Documentation Support
    1. 11.1 Device Support
      1. 11.1.1 Device Nomenclature
    2. 11.2 Documentation Support
      1. 11.2.1 Related Documentation
    3. 11.3 Related Links
    4. 11.4 Community Resources
    5. 11.5 Trademarks
    6. 11.6 Electrostatic Discharge Caution
    7. 11.7 Glossary
  12. 12Mechanical, Packaging, and Orderable Information

パッケージ・オプション

メカニカル・データ（パッケージ｜ピン）
サーマルパッド・メカニカル・データ
発注情報

8 Application and Implementation

NOTE

Information in the following applications sections is not part of the TI component specification, and TI does not warrant its accuracy or completeness. TI’s customers are responsible for determining suitability of components for their purposes. Customers should validate and test their design implementation to confirm system functionality.

8.1 Application Information

In the design of any application involving a high-speed data converter, particular attention should be paid to the design of the analog input, the clocking solution, and careful layout of the clock and analog signals. The ADS5562 evaluation module (EVM) is one practical example of the design of the analog input circuit and clocking solution, as well as a practical example of good circuit board layout practices around the ADC.

8.2 Typical Application

The analog inputs of the ADS5562 device must be fully differential and biased to an appropriate common mode voltage, VCM. End equipment typically does not have a signal that already meets the requisite amplitude and common mode and is fully differential. Therefore, a signal conditioning circuit is required for the analog input. If the amplitude of the input circuit is such that no gain is needed to make full use of the full-scale range of the ADC, then a transformer coupled circuit as used on the EVM can be used with good results. The transformer coupling is inherently low-noise, and inherently AC-coupled so that the signal may be biased to VCM after the transformer coupling. Figure 59 shows an example of transformer coupling as used on the ADS556x EVM.

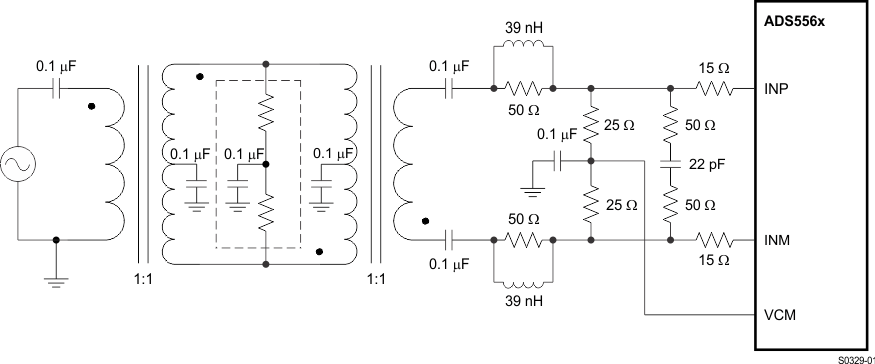ADS5560 ADS5562 s0329-01_lws207.gif Figure 59. Drive Circuit Using RF Transformers

If signal gain is required, or the input bandwidth is to include the spectrum all the way down to DC such that AC coupling is not possible, then an amplifier-based signal conditioning circuit would be required. Figure 60 shows the LMH6552 device interfaced with the ADS5562 device. The LMH6552 device is configured to have to single-ended input with a differential outputs follow by the first Nyquist-based low-pass filter with 40-MHz bandwidth. Figure 60 also shows the power supply recommendations for the amplifier.

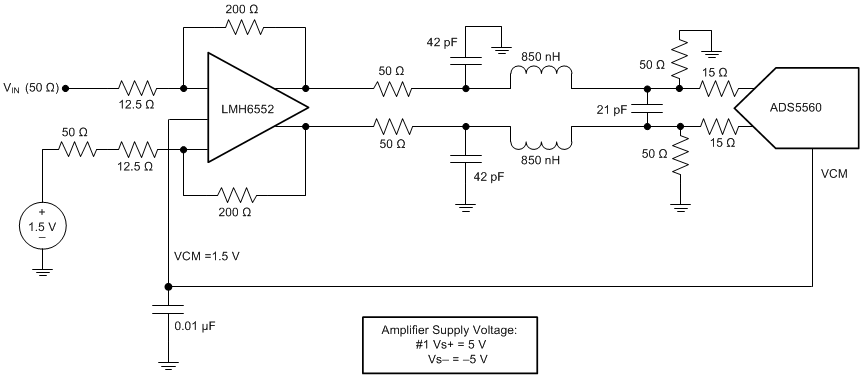ADS5560 ADS5562 LMH6552_ADS5560_typ_app.gif Figure 60. Drive Circuit Using LMH6552 Fully Differential Amplifier

Clocking a high-speed ADC such as the ADS5562 device requires a fully differential-clock signal from a clean, low-jitter clock source and driven by an appropriate clock buffer, often with LVPECL or LVDS signaling levels. The sample clock must also be biased up to the appropriate common mode voltage, but unlike the analog input, the data converter itself will often internally bias the clock to the appropriate VCM if the clock signal is AC coupled as in the typical clock driver circuit shown in Figure 50 through Figure 53.

8.2.1 Design Requirements

The ADS5562 device requires a fully differential analog input with a full-scale range not to exceed 3.56-V peak-to-peak differential, biased to a common-mode voltage of 1.5 V. In addition the input circuit must provide proper transmission line termination (or proper load resistors in an amplifier-based solution) so the input of the impedance of the ADC analog inputs should be considered as well.

The ADS5562 device is capable of a typical SNR of 82.8 dBFS for input frequencies of about 30 MHz, which is well under the Nyquist limit for this ADC operating at 80 Msps. The amplifier and clocking solution have a direct impact on performance in terms of SNR. Therefore the amplifier and clocking solution should be selected such that the SNR performance of at least 82 dBFS is preserved.

8.2.2 Detailed Design Procedure

The ADS5562 device has a maximum sample rate of 80 MHz and an input bandwidth of approximately 300 MHz. For this application, the first Nyquist zone is involved, so the frequency bandwidth must be limited under 40 MHz.

8.2.2.1 Clocking Source for ADC5562

The signal-to-noise ratio of the ADC is limited by three different factors: the quantization noise, the thermal noise, and the total jitter of the sample clock. Quantization noise is driven by the resolution of the ADC, which is 16 bits for the ADS5562 device. Thermal noise is typically not noticeable in high-speed pipelined converters such as the ADS5562 device, but may be estimated by looking at the signal to noise ratio of the ADC with very-low input frequencies and using Equation 3 to solve for thermal noise. For this estimation, use the specified SNR for the lowest frequency listed (see the Specifications section. The lowest input frequency listed for the ADS5562 device is at 3 MHz, and the SNR at that frequency is 84 dB. Therefore, use 84 dB as the SNR limit for this application because of thermal noise. This value is just an approximation, and the lower the input frequency that has an SNR specification the better this approximation is. The thermal noise limits the SNR at low input frequencies while the clock jitter sets the SNR for higher input frequencies.

Quantization noise is also a limiting factor for SNR, as the theoretical maximum achievable SNR as a function of the number of bits of resolution is set by Equation 2.

Equation 2. ADS5560 ADS5562 equation_01_slws207.gif

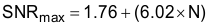
where

  • N = number of bits resolution.

For a 16-bit ADC, the maximum SNR = 1.76 + (6.02 × 16) = 98.08 dB. This value is the number that is entered into Equation 3 for quantization noise as we solve for total SNR for different amounts of clock jitter using Equation 3.

Equation 3. ADS5560 ADS5562 eq_01_slas611.gif

Use Equation 4 to calculate the SNR limitation because of sample clock jitter.

Equation 4. ADS5560 ADS5562 eq_02_slas611.gif

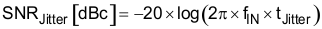
Note that the clock jitter in Equation 4 is the total amount of clock jitter, whether the jitter source is internal to the ADC or external because of the clocking source. The total clock jitter (TJitter) has two components – the internal aperture jitter (90 fs for ADS5562) which is set by the noise of the clock input buffer, and the external clock jitter from the clocking source and all associated buffering of the clock signal. Use Equation 5 to calculate the total clock jitter from the aperture jitter and the external clock jitter.

Equation 5. ADS5560 ADS5562 eq_03_slas611.gif

The external clock jitter can be minimized by using high-quality clock sources and jitter cleaners as well as a bandpass filter at the clock input while a faster clock slew rate may at times also improve the ADC aperture jitter slightly.

The ADS5562 device has an internal aperture jitter of 90 fs, which is largely fixed. The SNR depending on amount of external jitter for different input frequencies is shown in Figure 61. Often the design requirements list a target SNR for a system, and Equation 3 through Equation 5 are then used to calculate the external clock jitter needed from the clocking solution to meet the system objectives.

Figure 61 shows that with an external clock jitter of 200 fs rms, the expected SNR of the ADS5562 device is greater than 82 dBFS at an input tone of 40 MHz, which is the Nyquist limit. Having less external clock jitter such as 150 fs rms, or even 100 fs rms, results in an SNR that exceeds the design target, but possibly at the expense of a more costly clocking solution. An external clock jitter of greater than 200 fs does not meet the design target. Because the design target for SNR is established at 82 dB, and a margin of error is necessary for the SNR contribution from the amplifier and filter on the analog signal, the design goal of 150 fs external clock jitter is established to achieve an SNR for the ADC of approximately 83 dB.

8.2.2.2 Amplifier Selection

The amplifier and any input filtering has its own SNR performance, and the SNR performance of the amplifier front end combines with the SNR of the ADC to yield a system SNR that is less than that of the ADC. System SNR can be calculated from the SNR of the amplifier conditioning circuit and the overall ADC SNR as in Equation 6. In Equation 6, the SNR of the ADC is the value derived from the data sheet specifications and the clocking derivation presented in the Clocking Source for ADC5562 section.

Equation 6. ADS5560 ADS5562 eq_04_slas611.gif

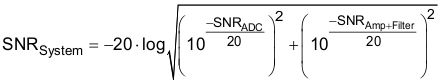
The SNR of the amplifier and filter can be calculated from the noise specifications in the data sheet for the amplifier, the amplitude of the signal and the bandwidth of the filter. The noise from the amplifier is band-limited by the filter, and the rolloff of the filter depends on the order of the filter. Therefore, replacing the filter rolloff with an equivalent brick-wall filter bandwidth is convenient. For example, a 1st order filter can be approximated by a brick-wall filter with bandwidth of 1.57 times the bandwidth of the 1st order filter. For this design, assume a 1st order filter is used. Use Equation 7 to calculate the amplifier and filter noise.

Equation 7. ADS5560 ADS5562 eq_05_slas611.gif

where

  • VO = the amplifier output signal (which will be full scale input of the ADC expressed in rms)
  • EFILTEROUT = ENAMPOUT × √ENB
    • ENAMPOUT = the output noise density of the LMH6552 (1.1 nV/√Hz times amplifier gain)
    • ENB = the brick-wall equivalent noise bandwidth of the filter

In Equation 7, the parameters of the equation may be seen to be in terms of signal amplitude in the numerator and amplifier noise in the denominator, or SNR. For the numerator, use the full-scale voltage specification of the ADS5562 device, or 3.56-V peak-to-peak differential. Because Equation 7 requires the signal voltage to be in rms, convert 3.56 VPP to 1.26 V rms.

The noise specification for the LMH6552 device is listed as 1.1 nV/√Hz times the amplifier gain. Therefore, use this value to integrate the noise component from DC out to the filter cutoff, using the equivalent brick wall filter of 40 MHz × 1.57, or 62.8 MHz. The result of 1.1 nV/√Hz over √62.8 MHz times gain yields 8717 nV, or 8.717 µV, assuming a gain factor of 2 for the amplifier.

Using 1.26-V rms for VO and 8.717 µV for EFILTEROUT, the SNR of the amplifier and filter as given by Equation 7 is approximately 103.2 dB.

Taking the SNR of the ADC as 83 dB from Figure 61, and SNR of the amplifier and filter as 103.2 dB, Equation 6 predicts the system SNR to be 82.96 dB. In other words, the SNR of the ADC and the SNR of the front end combine as the square root of the sum of squares, and because the SNR of the amplifier front end is much greater than the SNR of the ADC in this example, the SNR of the ADC dominates Equation 6 and the system SNR is almost the SNR of the ADC. The assumed design requirement is 82 dB, and after a clocking solution was selected and an amplifier or filter solution was selected, the predicted SNR of is 82.96 dB. At this point, consider making tradeoffs of either the clocking specification or amplifier gain to see how such tradeoffs begin to affect the expected system performance.

8.2.3 Application Curve

Figure 61 shows the SNR of the ADC as a function of clock jitter and input frequency for the ADS5562 device. This plot of curves take into account the aperture jitter of the ADC, the number of bits of resolution, and the thermal noise estimation so that the plot can be used to predict SNR for a given input frequency and external clock jitter. Figure 61 then may be used to set the jitter requirement for the clocking solution for a given input bandwidth and given design goal for SNR.

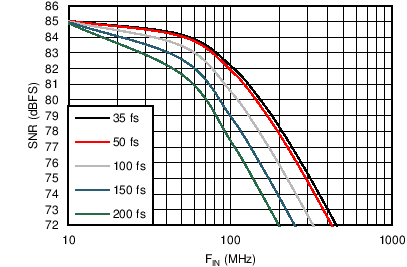ADS5560 ADS5562 C001_SLWS207.png Figure 61. SNR vs Input Frequency and External Clock Jitter